11.3 Distance-Based Weights
With a definition of distance in hand, neighbors can be defined as those pairs of points that are within a critical cut-off distance from each other. Alternatively, the k closest points, or k-nearest neighbors can be selected. These approaches can be readily extended to more general concepts of distance.
11.3.1 Distance-band weights
The most straightforward spatial weights matrix constructed from a distance measure is obtained when \(i\) and \(j\) are considered neighbors whenever \(j\) falls within a critical distance band from \(i\). More precisely, \(w_{ij} = 1\) when \(d_{ij} \le \delta\), and \(w_{ij} = 0\) otherwise, where \(\delta\) is a preset critical distance cutoff.
In order to avoid isolates (islands) that would result from too stringent a critical distance, the distance must be chosen such that each location has at least one neighbor. Such a distance conforms to a max-min criterion, i.e., it is the largest of the nearest neighbor distances.75
In practice, the max-min criterion often leads to too many neighbors for locations that are somewhat clustered, since the critical distance is determined by the points that are farthest apart. This problem frequently occurs when the density of the points is uneven across the data set, such as when some of the points are clustered and others are more spread out. This is examined more closely in the illustrations.
11.3.2 K-nearest neighbor weights
With a full matrix of inter-point distances \(D\), each \(i\)-th row contains the distances between a point \(i\) and all other points \(j\). With these distances sorted from smallest to largest, as \(d_{ij}^*\), a concept of k-nearest neighbors can be defined.
For each \(i\), the k-nearest neighbors are those \(j\) with \(d_{ij}^*\) for \(j = 1,k\), i.e., the k closest points (this assumes there are no ties, which is considered below). This is not a symmetric relationship. Even though \(d_{ij} = d_{ji}\) the sorted order of distances for \(i\) is often not the same as the sorted order for \(j\).
Imagine the situation with three points on a line as A, B and C, with C closer to B than A is to B. Then B will be the nearest neighbor for A, but A will not be the nearest neighbor for B. This asymmetry can cause problems in analyses that depend on the intrinsic symmetry of the weights (e.g., some algorithms to estimate spatial regression models).
Another potential issue with \(k\)-nearest neighbor weights is the
occurrence of ties, i.e., when more than one location \(j\) has the
same distance from \(i\). A number of solutions exist to break
the tie, from randomly selecting one of the \(k\)-th order
neighbors, to including all of them. In GeoDa,
random selection is implemented.
To illustrate these properties, consider Figure 11.1, portraying six points. The nearest neighbor relation is shown by an arrow from \(i\) to \(j\). For example, E is clearly the nearest neighbor of C, but C is not the nearest neighbor for E (that is F). The triangle D-A-B illustrates the problem of ties. D is equidistant from A and B, so it is impossible to pick one or the other as the nearest neighbor. On the other hand, the nearest neighbor relation between A and B is symmetric (arrow in both directions).
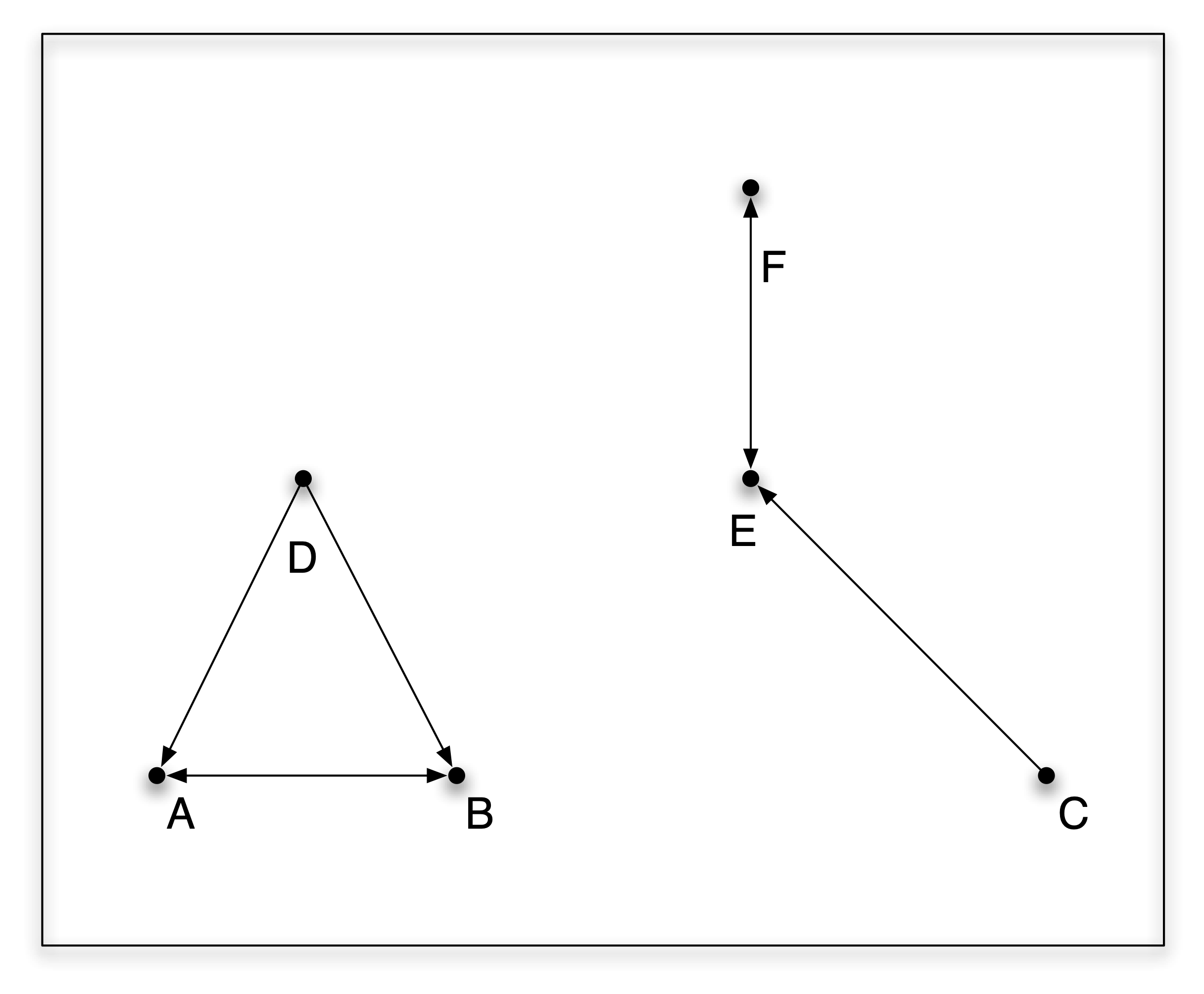
Figure 11.1: Nearest neighbor properties
In practice, k-nearest neighbor weights often provide a solution to the problem of isolates, since they ensure that each observation has exactly k neighbors (see Section 11.4.2). However, this approach should not be applied uncritically. One drawback of the concept is that it warps the effect of distance.
For sparsely distributed points, the nearest neighbor (and, by extension, the k nearest neighbors) can be quite far removed, whereas for densely distributed points, many neighbors can be found within a small distance band. In terms of interaction, this implies that the actual distance is of less relevance than the fact that a neighbor is encountered, which is not always an appropriate assumption. For example, when considering commuting distances, a destination 40 miles away may be a reasonable neighbor, whereas there may be very little interaction with a nearest neighbor that is 150 miles away.
Since the k-nearest neighbor relationship is typically asymmetric, it is sometimes desired to convert this to symmetric spatial weights. One approach to accomplish this is to replace the original weights matrix \(\mathbf{W}\) by \((\mathbf{W + W'})/2\), which is symmetric by construction.76 Each new weight is then \((w_{ij} + w_{ji})/2\). The resulting matrix will have more neighbors than the original knn weights.
An alternative approach is to only use the instances where \(w_{ij} = w_{ji} = 1\). This is referred to as mutual symmetry. The result will be a much sparser weights matrix, with the possibility of isolates.
11.3.3 General distance weights
With a general concept of distance in attribute space, the implementation of distance-band and k-nearest neighbor weights is straightforward. However, when using a distance band, the meaning of the implied max-min distance is not always obvious, since it is a combination of distances among multiple variable dimensions.
An alternative weights construction is sometimes considered as the inverse of the generalized distance: \[ w_{ij} = 1 / | z_{i} - z_{j} |^{\alpha} = | z_{i} - z_{j} |^{-\alpha}, \]
or, in standardized form: \[ w_{ij} = \frac{| z_{i} - z_{j} |^{-\alpha}}{\sum_{j} | z_{i} - z_{j} |^{-\alpha}}. \]
For example, in the much cited study by Case, Rosen, and Hines (1993), two separate weights matrices were constructed using economic weights. One was based on the difference in per capita income between states and the other on the difference in the proportion of their Black population. In another nice example, Greenbaum (2002) uses the concept of a similarity matrix to characterize school districts that are similar in per-student income. Instead of using those weights as such, they are combined with a nearest neighbor distance cut-off, so that the similarity weight is only computed when the school districts are also within a given order of geographic nearest neighbors (see also the discussion of weights intersection in Section 11.6.1).
Weights created as functions of distance are further considered in Chapter 12.