8.2 Spectral Clustering Logic

Clustering methods like K-Means, K-Medians or K-Medoids are designed to discover convex clusters in the multidimensional data cloud. However, several interesting cluster shapes are not convex, such as the classic textbook spirals (Figure 8.1) or moons examples, or the famous Swiss roll and similar lower dimensional shapes embedded in a higher dimensional space.

These problems are characterized by a property that projections of the data points onto the original orthogonal coordinate axes (e.g., the X, Y, Z, etc. axes) do not create good separations. Spectral clustering approaches this issue by reprojecting the observations onto a new axes system and carrying out the clustering on the projected data points. Technically, this will boil down to the use of eigenvalues and eigenvectors, hence the designation as spectral clustering (see Section 2.2.2.1).

To illustrate the problem, consider the result of K-Means and K-Medoids (for \(k=2\)) applied to the famous spirals data set from Figure 8.1. As Figure 8.2 shows, these methods tend to yield convex clusters, which fail to detect the nonlinear arrangement of the data. The K-Means clusters are arranged above and below a diagonal, whereas the K-Medoids result shows more of a left-right pattern.

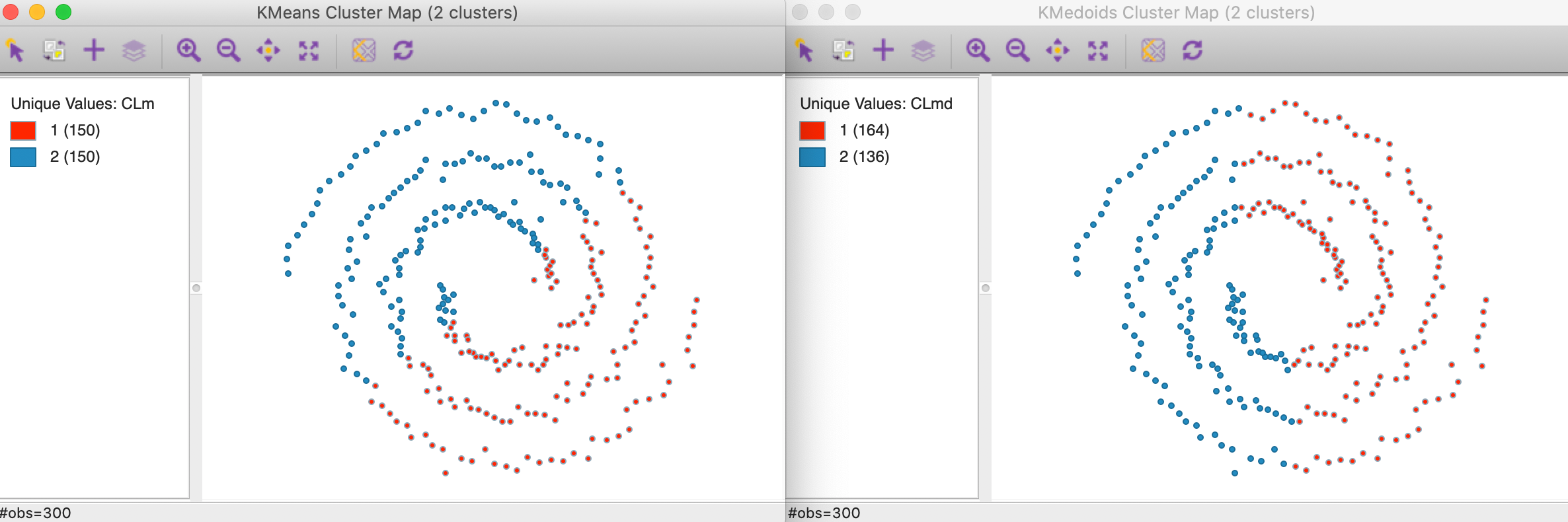
Figure 8.2: K-Means and K-Medoids for Spirals Data

In contrast, as shown in Figure 8.3, a spectral clustering algorithm applied to this data set perfectly extracts the two underlying patterns (initialized with a knn parameter of 3, see Section 8.4.3).

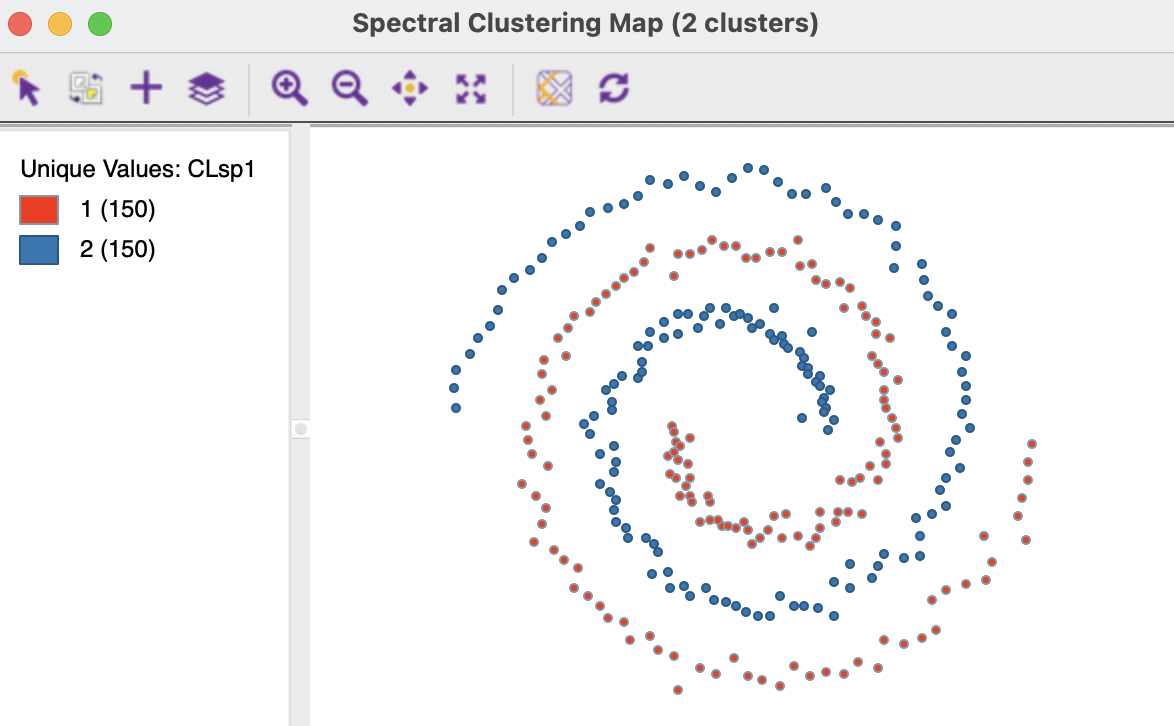
Figure 8.3: Spectral Clustering of Spirals Data

The mathematical solution underlying spectral clustering is based on a graph partitioning logic. More specifically, the clusters are viewed as subgraphs of a graph that represents the data structure. The subgraphs are internally well connected, but only weakly connected with the other subgraphs. Technical details can be found in the exhaustive overview of the various mathematical properties associated with spectral clustering contained in the tutorial by von Luxburg (2007).

In the remainder of the chapter, the graph partitioning idea is discussed first, followed by an overview of the main steps in a spectral clustering algorithm, including a review of some important parameters that need to be tuned in practice. The section closes with an illustration of its implementation, options and sensitivity analysis.