3.3 SMACOF
SMACOF stands for “scaling by majorizing a complex function.” The method was initially suggested by de Leeuw (1977) as an alternative to the gradient descent method that was typically employed to minimize the MDS stress function. It was motivated in part because the eigenvalue approach outlined above for classic metric MDS does not work unless the distance function is Euclidean. In many early applications of MDS in psychometrics this was not the case.
The idea behind the iterative majorization method is actually fairly straightforward, but its implementation can be quite complex. In essence, a majorizing function must be found that is much simpler than the original function, and, for a minimization problem, is always above the actual function.
With a function \(f(x)\), a majorizing function \(g(x,z)\) is such that for a fixed point \(z\) the two functions are equal, such that \(f(z) = g(z,z)\) (\(z\) is called the supporting point). The auxiliary function should be easy to minimize (easier than \(f(x)\)) and always dominate the original function, such that \(f(x) \leq g(x,z)\). This leads to the so-called sandwich inequality (coined as such by de Leeuw): \[f(x^*) \leq g(x^*,z) \leq g(z,z) = f(z),\] where \(x^*\) is the value that minimizes the function \(g\).
The iterative part stands for the way in which one proceeds. One starts with a value \(x_0\), such that \(g (x,x_0) = f(x_0)\). For example, consider a parabola that sits above a complex nonlinear function and is tangent to it at \(x_0\), as shown in Figure 3.7.12 One can easily find the minimum for the parabola, say at \(x_1\).
Next, a new parabola is moved such that it is tangent to the function at \(x_1\), with again \(g(x,x_1) = f(x_1)\). In the following step, the minimum for the new parabola is found at \(x_2\). The procedure continues in this iterative fashion until the difference between \(x_k\) and \(x_{k-1}\) for two consecutive steps is less than a critical value (the convergence criterion). At that point the minimum of the parabola is considered to sufficiently approximate the minimum for the function \(f(x)\), given a convergence criterion.
Figure 3.7: Iterative Majorization
3.3.1 Mathematical Details
The application the SMACOF approach to find the minimum of the stress function is quite complex, and the full technical details are beyond the current scope.13 The main challenge is to find a suitable majorizing function for the stress function: \[S(Z) = \sum_{i < j} (\delta_{ij} - d_{ij}(Z))^2 = \sum_{i<j} \delta_{ij}^2 + \sum_{i<j} d_{ij}^2(Z) - 2 \sum_{i<j} \delta_{ij}d_{ij}(Z),\] where \(Z\) is a matrix with the solution to the MDS problem, \(\delta_{ij}\) is the distance between \(i\) and \(j\) for the original configuration, and \(d_{ij}(Z)\) is the corresponding distance for a proposed solution \(Z\). In general, \(\delta_{ij}\) can be based on any distance metric or dissimilarity measure, but \(d_{ij}(Z)\) has to be a Euclidean distance.
In the stress function, the first term, pertaining to \(\delta_{ij}\) (the original inter-observation distances), is a constant, since it does not change with the values for the coordinates in \(Z\). The second term is a sum of squared distances between pairs of points in \(Z\), and the third term is a weighted sum of the pairwise distances (each weighted by the initial distances). The objective is to find a set of coordinates \(Z\) that minimizes \(S(Z)\).
To turn the stress function into a matrix expression suitable for the application of the majorization principle, some special notation is introduced. The difference between observation \(i\) and \(j\) for a column \(h\) in \(Z\), \(z_{ih} - z_{jh}\), can be written as \((e_i - e_j)'Z_h\), where \(e_i\) and \(e_j\) are, respectively, the \(i\)-th and \(j\)-th column of the identity matrix, and \(Z_h\) is the \(h\)-th column of \(Z\). As a result, the squared difference between \(i\) and \(j\) for column \(h\) follows as \(Z_h'(e_i - e_j)(e_i - e_j)'Z_h\). In the MDS literature, the notation \(A_{ij}\) is used for the \(n \times n\) matrix formed by \((e_i - e_j)(e_i - e_j)'\). This is a special matrix consisting of all zeros, except for \(a_{ii} = a_{jj} = 1\) and \(a_{ij} = a_{ji} = -1\).
Considering all column dimensions of \(Z\) jointly then gives the squared distance between \(i\) and \(j\) as: \[d^2_{ij}(Z) = \sum_{h=1}^k z_h'A_{ij}z_h = tr Z'A_{ij}Z,\] with \(tr\) as the trace operator (the sum of the diagonal elements). Furthermore, summing this over all the pairs \(i-j\) (without double counting) gives: \[\sum_{i<j} d_{ij}^2(Z) = tr(Z' \sum_{i <j}A_{ij}Z) = tr(Z'VZ),\] with the \(n \times n\) matrix \(V = \sum_{i <j}A_{ij}\), a row and column centered matrix (i.e., each row and each column sums to zero), with \(n - 1\) on the diagonals and \(-1\) in all other positions. Given the row and column centering, this matrix is singular.
The third term, \(- 2 \sum_{i<j} \delta_{ij}d_{ij}(Z)\) is the most complex, and the place where the majorization comes into play. Using the same logic as before, it can be written as \(-2 tr[Z'B(Z)Z]\), where \(B(Z)\) is a matrix with off-diagonal elements \(B_{ij} = - \delta_{ij} / d_{ij}(Z)\), and diagonal elements \(B_{ii} = - \sum_{j, j\neq i} B_{ij}\). In the matrix \(B\), the diagonal elements equal the sum of the absolute values of all the column/row elements, so that rows and columns sum to zero, i.e., the matrix \(B\) is double centered.
The majorization is introduced by considering a candidate set of coordinates as \(Y\). After some complex manipulations, a majorization condition follows, which relates the candidate coordinates \(Y\) to the solution \(Z\) through the so-called Guttman transform.14 This transform expresses an updated solution \(Z\) as a function of a tentative solution to the majorizing condition, \(Y\), through the following equality: \[Z = (1/n)B(Y)Y,\] where \(B(Y)\) has the same structure as \(B(Z)\) above, but now using the candidate coordinates from \(Y\).
In practice, the majorization algorithm boils down to an iteration over a number of simple steps:
start by picking a set of (random) starting values for \(Z\) and set \(Y\) to these values
compute the stress function for the current value of \(Z\)
find a new value for \(Z\) by means of the Guttman transform, using the computed distances included in \(B(Y)\), based on the current value of \(Y\)
update the stress function and check its change; stop when the change is smaller than a pre-set difference
if convergence is not yet achieved, set \(Y\) to the new value of \(Z\) and proceed with the update of the stress function
continue until convergence.
3.3.2 Implementation
The SMACOF approach is selected by specifying smacof as the Method in the interface of Figure 3.2. With this selection, the Maximum # of iterations and the Convergence Criterion options become available (those options are not available to the default classic metric method). The default setting is for 1000 iterations and a convergence criterion of 0.000001. These settings should be fine for most applications, but they may need to be adjusted if the minimization is not accomplished by the maximum number of iterations.
As in the classic metric case, after selecting variable names for the two dimensions (here, V1s and V2s), a scatter plot is provided, with the method listed in the banner, as in Figure 3.8.
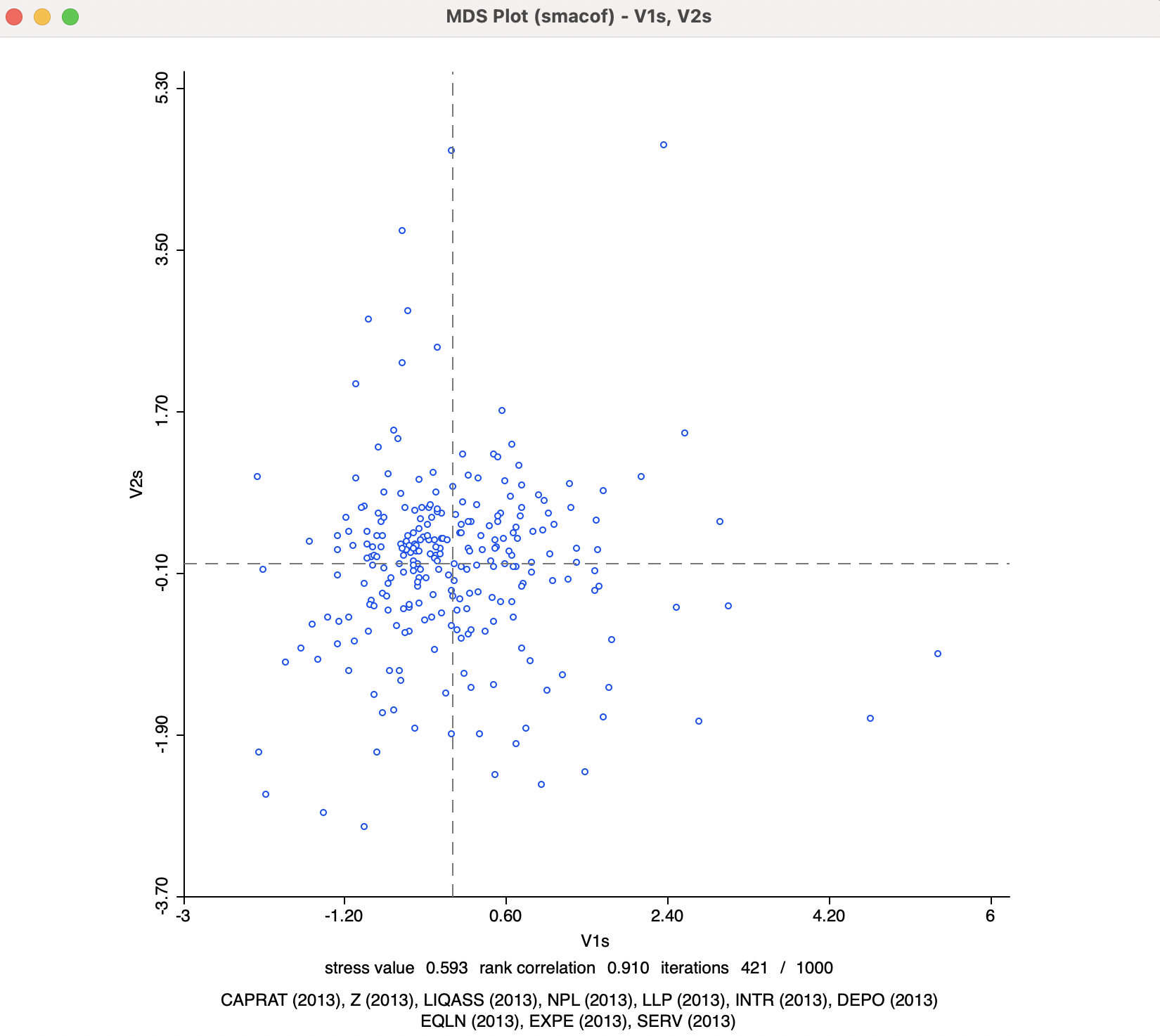
Figure 3.8: MDS Scatter Plot for SMACOF
Again, summary statistics of fit are listed at the bottom. In the example, the stress value is poorer than the classic metric solution, at 0.593 (relative to 0.394 in Figure 3.3), but the rank correlation is better, at 0.910 (relative to 0.084). It is also shown that convergence (for the default criterion) was reached after 421 iterations.
A result of 1000/1000 iterations would indicate that convergence has not been reached. In such an instance, the default number of iterations should be increased. Alternatively, the convergence criterion could be relaxed, but that is not recommended
The overall point pattern of Figure 3.8 is similar to that in Figure 3.3, but it is flipped. A closer investigation of similarities and differences can be carried out by linking and brushing. This will reveal a totally different orientation of the points, with opposite signs for both axes (see also Section 3.3.2.2).
3.3.2.1 Manhattan block distance
With the smacof method selected, the Manhattan block distance option becomes available as the Distance Function. As a result, the original inter-observation distances are based on absolute differences instead of squared differences. The resulting scatter plot (with variable names V1sm and V2sm) is shown in Figure 3.9. The main effect is to lessen the impact of outliers, or large distances in the original high dimensional space.
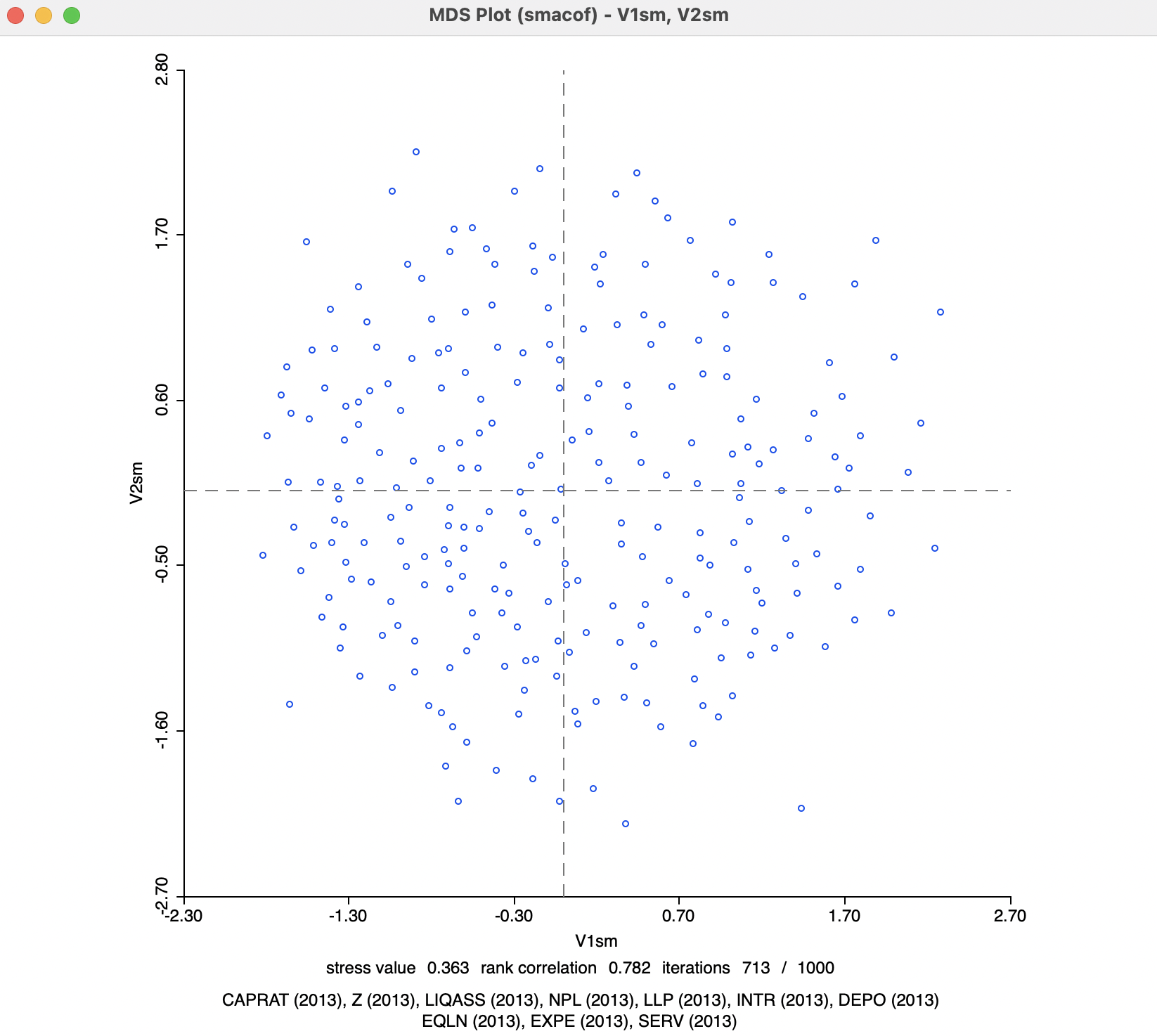
Figure 3.9: MDS Scatter Plot for SMACOF with Manhattan Distance
The result that follows from a Manhattan distance metric is quite different from the default Euclidean SMACOF plot in Figure 3.8. Importantly, the scale of the coordinates is not the same, such that the range of values on both axes is much smaller than in the Euclidean case. As a result, even if the points look farther apart, they are actually quite close on the scale of the original plot. However, the identification of close observations can differ considerably between the two plots. This can be further explored using linking and brushing.
In terms of fit, the stress value of 0.363 is better than for SMACOF with Euclidean distance, and even better than classic metric MDS, but the rank correlation of 0.782 is worse. Convergence is obtained after 713 iterations, substantially more than for the Euclidean distance option.
Overall, this means that the various MDS scatter plots should not be interpreted in a mechanical way, but careful linking and brushing should be employed to explore the trade-offs between the different options.
3.3.2.2 SMACOF vs classic metric MDS
A more formal comparison of the differences between the results for classic metric MDS and SMACOF (both for Euclidean distance) is provided by the scatter plots in Figure 3.10. On the left is a scatter plot that compares the x-axis, on the left one for the y-axis.
Clearly, the signs are opposite. While there is a close linear fit, with an \(R^2\) of 0.894 for the x-axis and 0.831 for the y-axis, there are also some substantial discrepancies, especially at the extreme values.
The advantage of the classic metric method is that its result has a direct relationship with principal components. On the other hand, the SMACOF method allows for the use of a Manhattan distance metric, which is less susceptible to the effect of observations that are far apart in the original multi-attribute space.
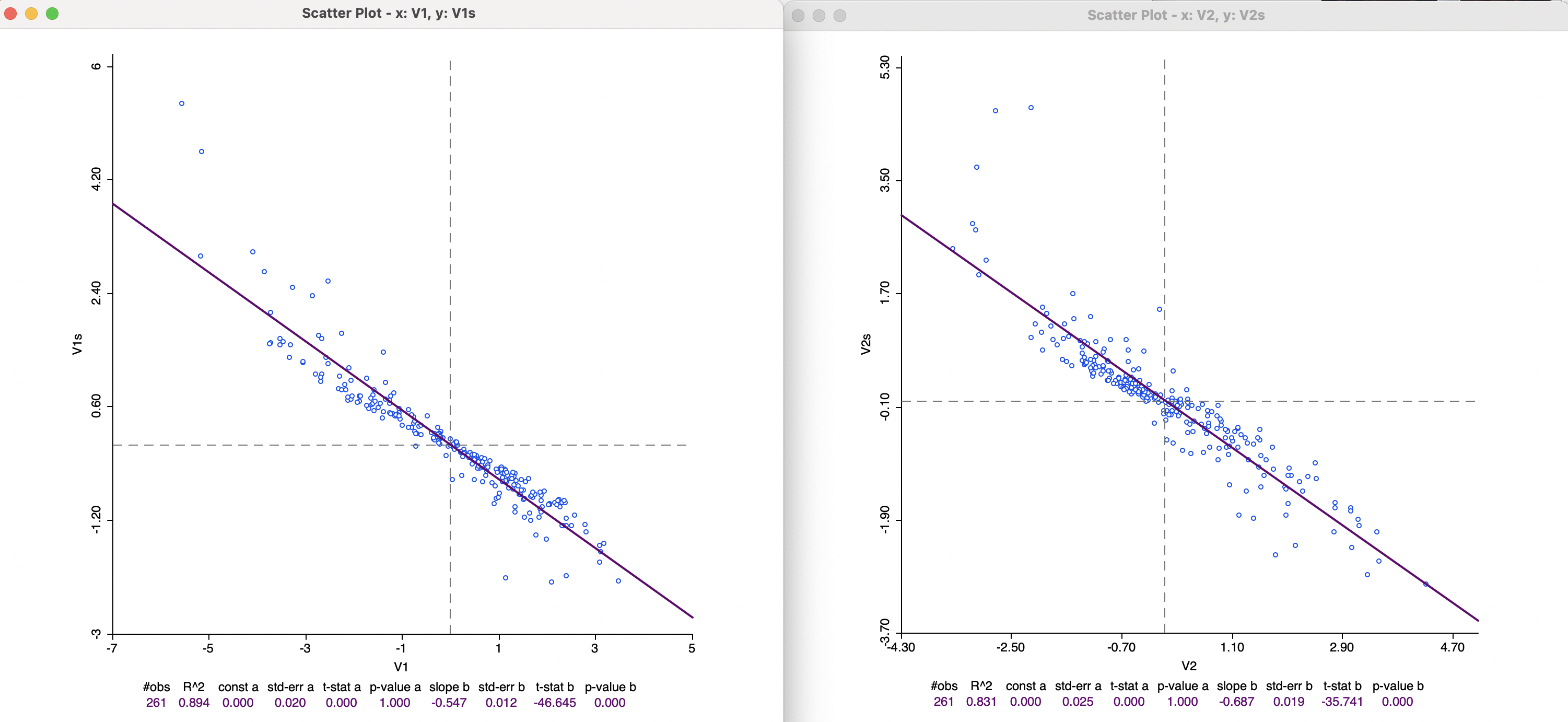
Figure 3.10: MDS Classic vs SMACOF Dimensions
For an extensive discussion, see Borg and Groenen (2005), Chapter 8, and de Leeuw and Mair (2009).↩︎
Technically, the majorization condition is based on the application of the Cauchy-Schwarz inequality, \(\sum_m z_my_m \leq (\sum_m z_m^2)^{1/2} (\sum_m y_m^2)^{1/2}\). Details can be found in Borg and Groenen (2005), Chapter 8.↩︎